The potential energy stored in a spring with spring constant
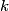 that is stretched a distance that is stretched a distance 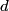 from its equilibrium position is from its equilibrium position is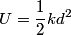 Let 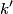 denote the spring constant of the second spring. Then, from the problem statement, denote the spring constant of the second spring. Then, from the problem statement,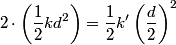 Solving for 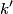 gives gives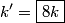 Therefore, answer (D) is correct. |